Entdecken Sie eine systematische Analyse von neun inspirierenden mathematischen Lernvorlagen, die mit EdrawMax erstellt und speziell für den deutschen Bildungskontext optimiert wurden. Alle Vorlagen entsprechen den aktuellen Bildungsstandards der Kultusministerkonferenz (KMK) und den Lehrplänen der deutschen Bundesländer – und das Beste: Sie können kostenlos online bearbeitet und individuell angepasst werden!
In diesem Artikel
- EdrawMax: Die ideale Plattform für mathematische Bildungsressourcen
-
- Uhrzeiten lesen – 5-Minuten-Genauigkeit (Primarstufe)
- Mathematik-Tafel – Bruchdarstellungen (Primarstufe)
- Pythagoreischer Lehrsatz – Übungssammlung (Sekundarstufe I)
- Mathematischer Überblick – Mindmap (Sekundarstufe I/II)
- Quadratische Funktionen und Parabeln (Sekundarstufe I/II)
- Flussdiagramm – Arithmetische Summenberechnung (Sekundarstufe II)
- Analytische Geometrie: Kreise und Dreiecke (Sekundarstufe II)
- Hasse-Diagramm für Mengen und Relationen (Sekundarstufe II)
- Hasse-Diagramm der Teilmengenrelation (Sekundarstufe II)
- Übersichtliche Vergleichstabelle
-
- Didaktische Hinweise
- Differenzierungsmöglichkeiten
- Digitale Integration
- Bewertungskriterien
- EdrawMax im Unterrichtseinsatz
- Praxisempfehlungen für den Einsatz
- Fazit und Ausblick
EdrawMax: Die ideale Plattform für mathematische Bildungsressourcen
EdrawMax revolutioniert die Erstellung mathematischer Lernmaterialien mit seiner benutzerfreundlichen und dennoch professionellen Diagramm-Software. Die Plattform begeistert mit einer intuitiven Benutzeroberfläche und speziell entwickelten Vorlagen für Geometrie, Flussdiagramme, Mindmaps und wissenschaftliche Diagramme. Besonders beeindruckend ist die nahtlose Integration verschiedener Darstellungsformen – von präzisen geometrischen Konstruktionen über komplexe Datenstrukturen bis hin zu motivierenden Visualisierungen.
Im deutschen Schulkontext eröffnet EdrawMax Lehrkräften völlig neue Möglichkeiten: die blitzschnelle Anpassung von Vorlagen an spezifische Lehrplaninhalte, während Schüler durch die kostenlose Online-Version eigenständig und kreativ mathematische Konzepte visualisieren und verstehen lernen. Die intelligenten Kollaborationsfunktionen fördern moderne Lernformen und unterstützen sowohl lebendigen Präsenzunterricht als auch effektiven Distanzunterricht.
Detaillierte Vorlagenanalyse
Die folgenden neun Lernvorlagen sind nach Schwierigkeitsgrad geordnet – von den ersten mathematischen Erfahrungen in der Grundschule bis hin zu anspruchsvollen Konzepten der Oberstufe. Jede Vorlage öffnet neue Türen zum mathematischen Verständnis!
1.1 Uhrzeiten lesen – 5-Minuten-Genauigkeit 🕐
a) Vorlagenbeschreibung
Dieses motivierende Arbeitsblatt verbindet spielerisch das Ablesen und Eintragen von Uhrzeiten auf analogen Zifferblättern. Einige Felder enthalten vorgegebene digitale Zeiten (z.B. 2:20, 4:25), für die Schüler die entsprechenden Zeiger präzise einzeichnen. Andere Felder zeigen bereits gezeichnete Zeiger, deren Zeit die Kinder in digitaler Form (hh:mm) notieren – ein perfektes Training für den Alltag!
b) Wissenschaftliche Prinzipien
- Winkelbeziehungen entdecken: 360°-Teilung des Kreises in 12 Stunden (30° pro Stunde) - Geometrie zum Anfassen!
- Proportionale Bewegung verstehen: Der Minutenzeiger bewegt sich 12-mal schneller als der Stundenzeiger
- Modulo-Arithmetik erleben: Spielerischer Einstieg in 12-Stunden- vs. 24-Stunden-System
- Koordinatensystem kennenlernen: Erste Erfahrungen mit polarer Darstellung von Zeigerpositionen
- Approximation üben: Sinnvolle Rundung auf 5-Minuten-Intervalle
c) Schulkontext
Zielgruppe: Primarstufe (Klassen 1-3), Förderschule, DaF-Unterricht
Lehrplanbezug: Perfekt abgestimmt auf die Grundschullehrpläne aller Bundesländer im Bereich "Größen und Messen". Erfüllt die KMK-Bildungsstandards für den Kompetenzbereich "Zeit".
Fächerintegration: Mathematik, Sachunterricht (Tagesablauf strukturieren), Deutsch als Fremdsprache
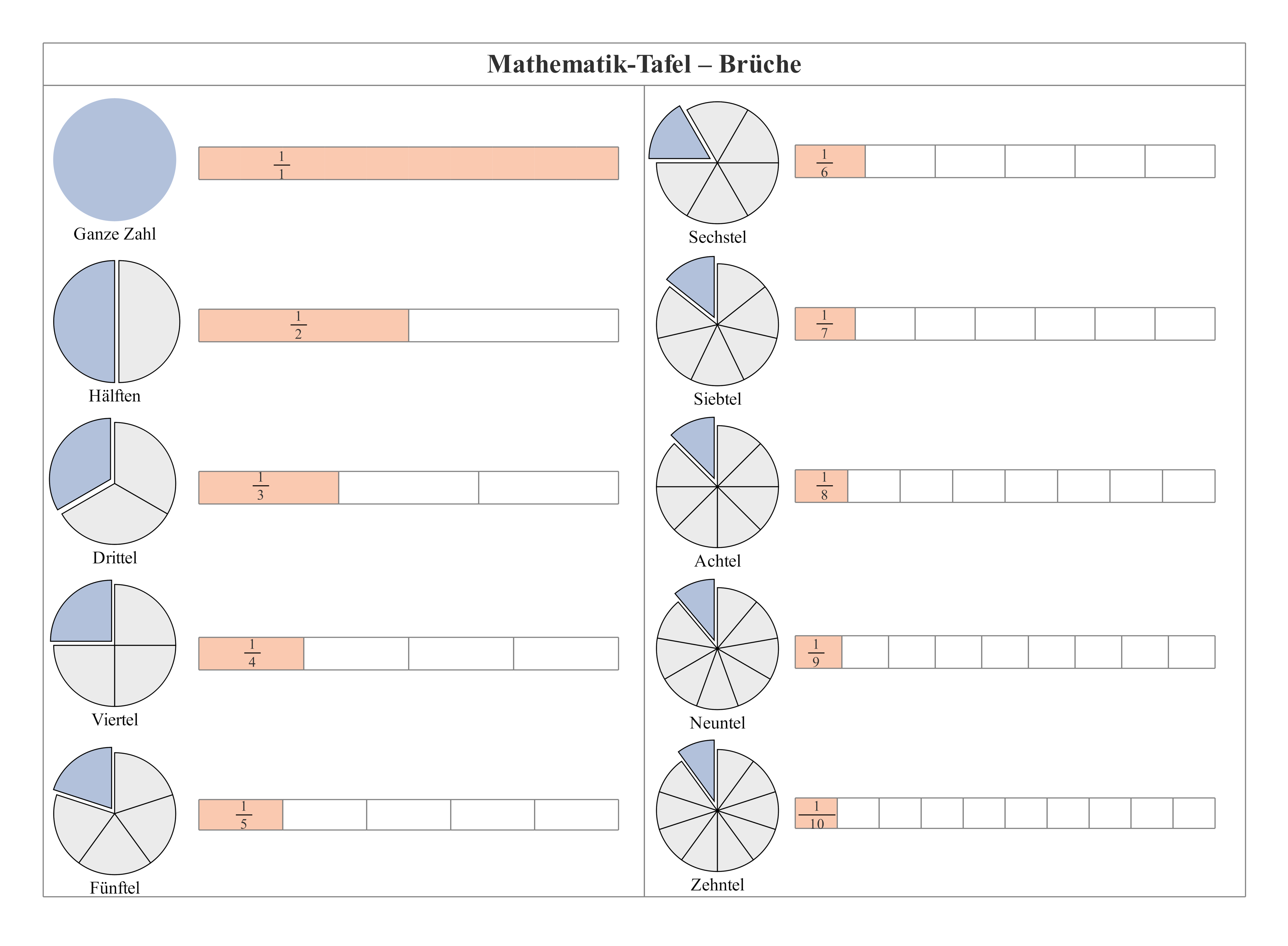
1.2 Mathematik-Tafel – Bruchdarstellungen 🍕
a) Vorlagenbeschreibung
Diese ansprechende Vorlage macht Brüche (1/2 bis 1/10) durch doppelte Visualisierung lebendig: Sowohl als farbenfrohe Kreisdiagramme als auch als übersichtliche Balkendiagramme. Jeder Bruch wird durch eingefärbte Segmente veranschaulicht, wobei die Gesamtfläche oder -länge immer die Einheit "1" repräsentiert. Diese duale Darstellung eröffnet verschiedene Zugänge zum Bruchverständnis und macht abstrakte Konzepte greifbar!
b) Wissenschaftliche Prinzipien
- Bruchkonzept entwickeln: Intuitive Teil-Ganzes-Verhältnisse und erste Äquivalenzklassen
- Dezimalentwicklung vorbereiten: Grundlagen für die Umwandlung zwischen Bruch- und Dezimaldarstellung
- Proportionalität erleben: Verhältnisse und Anteile in verschiedenen, lebensnahen Kontexten
- Flächeninhalt begreifen: Geometrische Interpretation von Brüchen durch visuelle Erfahrung
- Visuelle Mathematik fördern: Multiple Repräsentationen für nachhaltiges Verständnis
c) Schulkontext
Zielgruppe: Primarstufe (Klassen 3-4) und Sekundarstufe I (Klassen 5-6)
Lehrplanbezug: Kernbestandteil der Grundschullehrpläne aller Bundesländer im Bereich "Zahlen und Operationen". Orientiert sich an den bewährten KMK-Bildungsstandards für den Primarbereich.
Fächerintegration: Mathematik (Hauptfach), Sachunterricht (Alltagsbezug schaffen), Kunst (geometrische Formen gestalten)
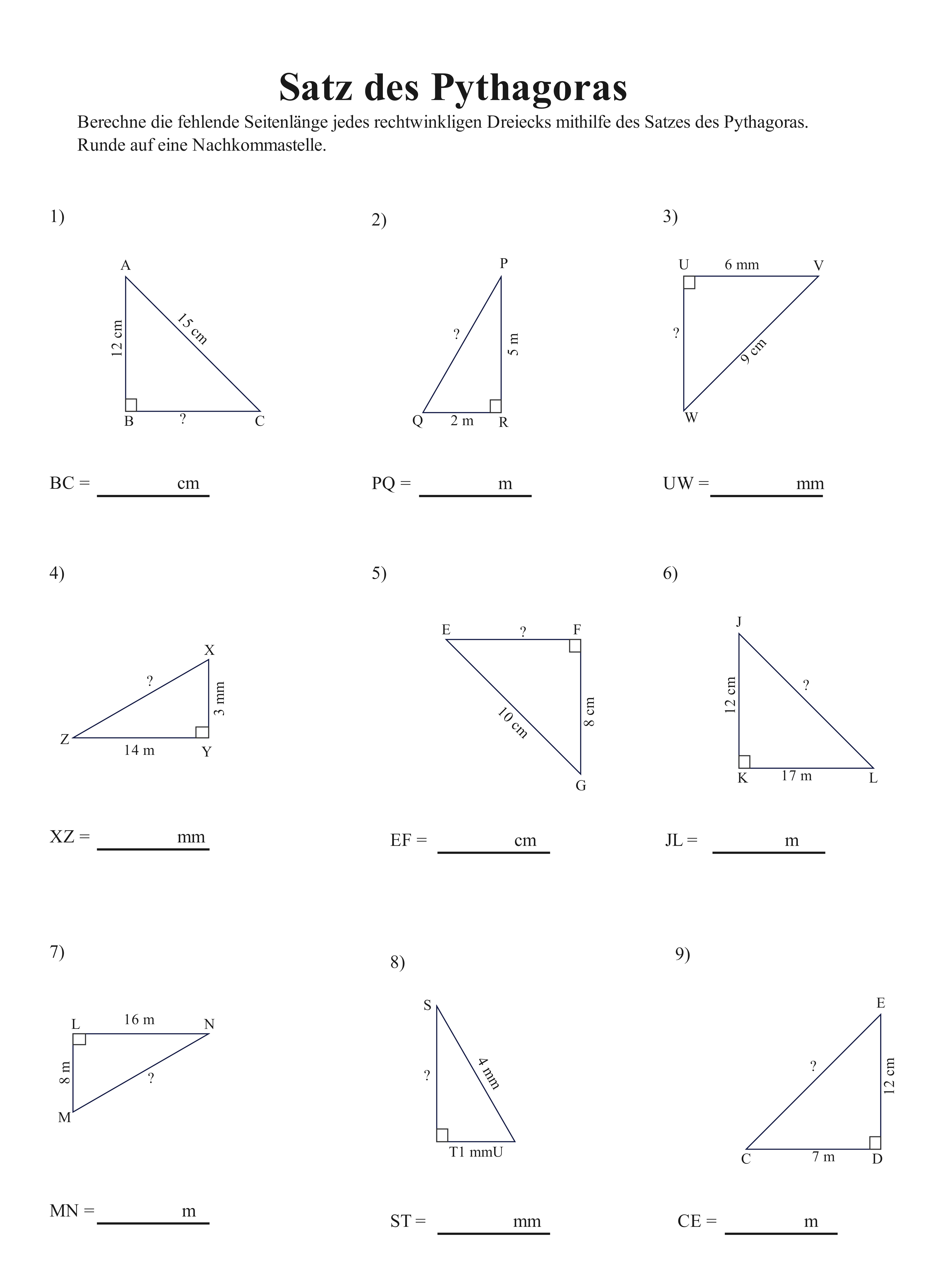
1.3 Pythagoreischer Lehrsatz – Übungssammlung 📐
a) Vorlagenbeschreibung
Diese systematisch aufgebaute Arbeitsblattsammlung präsentiert neun vielfältige Aufgaben zur praktischen Anwendung des berühmten Satzes von Pythagoras. Die Dreiecke sind bewusst in unterschiedlichen Orientierungen und Maßstäben dargestellt, mit variierten gegebenen und gesuchten Seitenlängen. Die präzise Rundung auf eine Nachkommastelle bereitet optimal auf weiterführende mathematische Berechnungen vor.
b) Wissenschaftliche Prinzipien
- Pythagoreischer Lehrsatz beherrschen: a² + b² = c² für rechtwinklige Dreiecke - ein Schlüssel zur Geometrie!
- Umkehrung verstehen: Eleganter Nachweis rechter Winkel durch Seitenlängenverhältnisse
- Raumdiagonalen berechnen: Spannendewendung in dreidimensionalen Körpern
- Trigonometrische Grundlagen schaffen: Solide Vorbereitung auf Sinus, Kosinus und Tangens
- Näherungsverfahren anwenden: Präzise Rundungsregeln und Genauigkeitsbetrachtungen
c) Schulkontext
Zielgruppe: Sekundarstufe I (Klassen 8-9), alle Schulformen
Lehrplanbezug: Zentraler Baustein der Kernlehrpläne aller Bundesländer im Bereich "Geometrie". Prüfungsrelevant für MSA/Realschulabschluss in allen deutschen Bundesländern.
Fächerintegration: Mathematik (Kernfach), Physik (Mechanik verstehen), Technik (präzise Konstruktion), Geographie (moderne Vermessung)
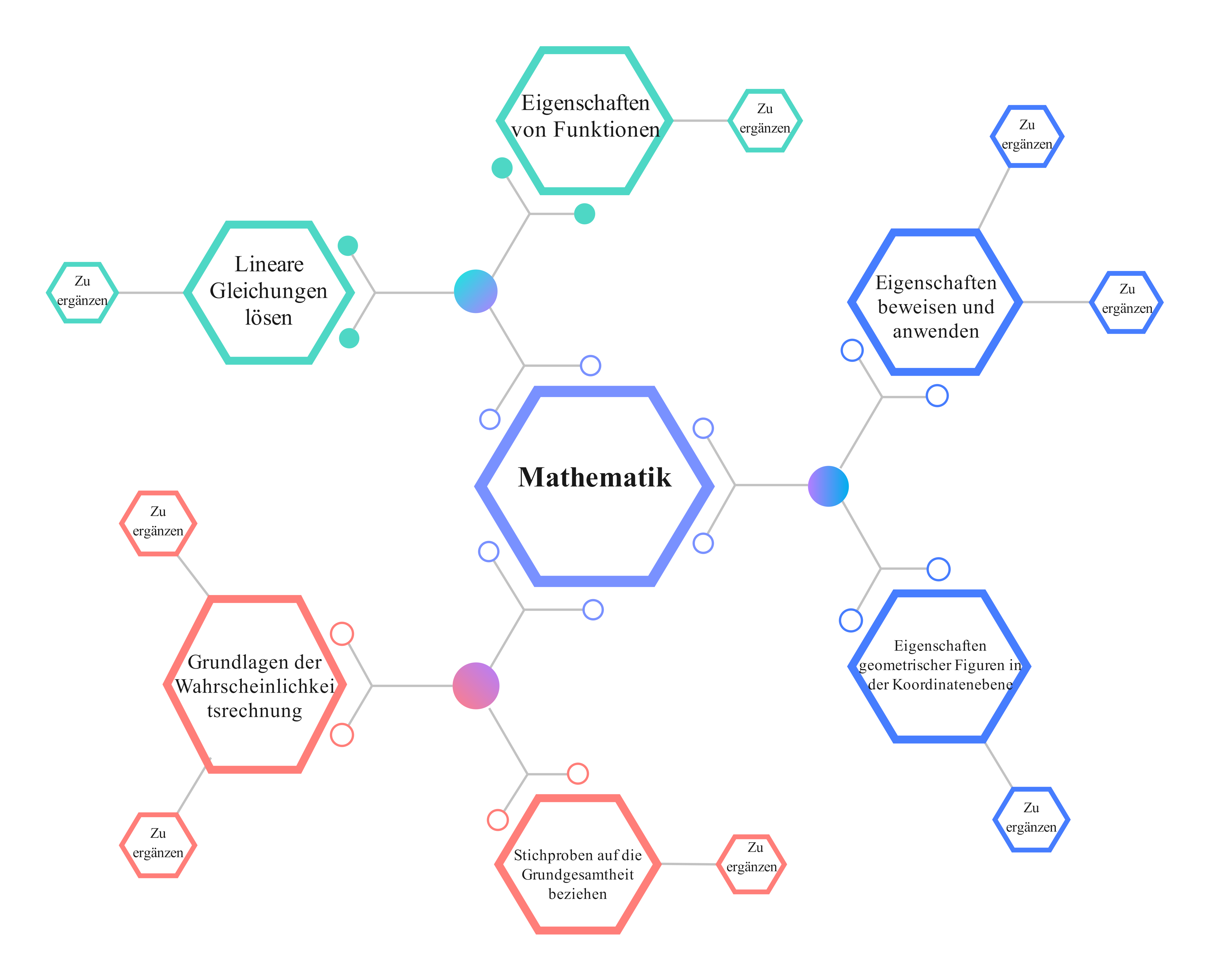
1.4 Mathematischer Überblick – Mindmap 🗺️
a) Vorlagenbeschreibung
Diese übersichtliche hexagonale Mindmap stellt "Mathematik" als inspirierenden zentralen Knoten dar, von dem sechs Hauptbereiche ausgehen: Lineare Gleichungen lösen, Eigenschaften von Funktionen erkunden, Eigenschaften beweisen und anwenden, Eigenschaften geometrischer Figuren entdecken, Stichproben auf Grundgesamtheit beziehen, und Grundlagen der Wahrscheinlichkeitsrechnung. Jeder Hauptbereich bietet Raum für weitere kreative Verzweigungen ("Zu ergänzen") - ein lebendiges Lernwerkzeug!
b) Wissenschaftliche Prinzipien
- Algebra entdecken: Gleichungen, Ungleichungen und faszinierende algebraische Strukturen
- Analysis erforschen: Funktionen, Grenzwerte, Differentiation und Integration verstehen
- Geometrie erleben: Euklidische und analytische Geometrie sowie praktische Trigonometrie
- Stochastik anwenden: Wahrscheinlichkeitstheorie und aussagekräftige beschreibende Statistik
- Beweistechniken beherrschen: Direkte, indirekte und konstruktive Beweise entwickeln
c) Schulkontext
Zielgruppe: Sekundarstufe I und II (Klassen 7-13), alle Schulformen
Lehrplanbezug: Übergreifende, strukturierende Darstellung der Kernlehrpläne aller Bundesländer. Systematisch entwickelt nach den sechs mathematischen Leitideen der KMK-Bildungsstandards.
Fächerintegration: Mathematik (strukturierende Übersicht), fächerübergreifende Projektarbeit fördern
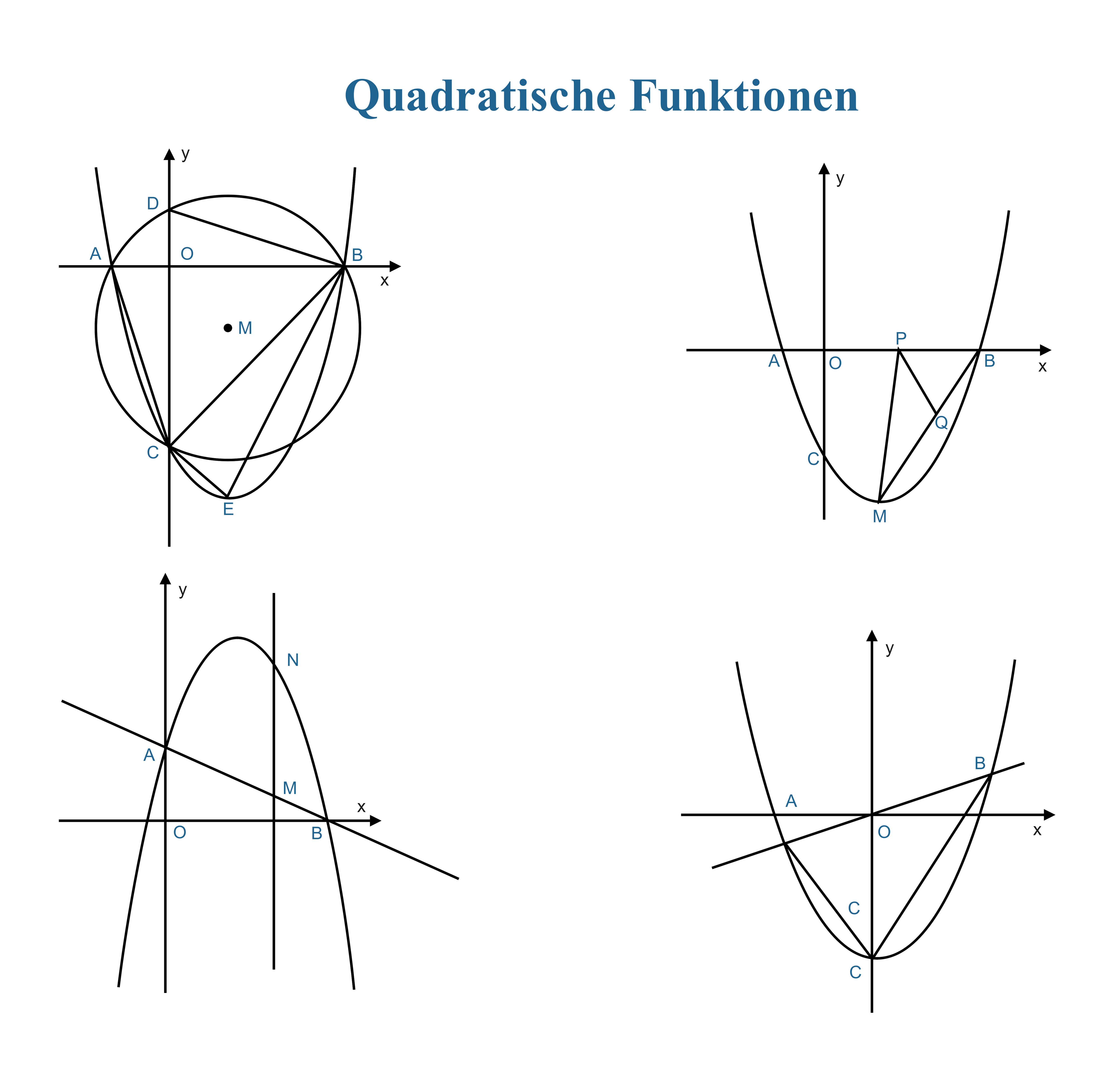
1.5 Quadratische Funktionen und Parabeln 📈
a) Vorlagenbeschreibung
Diese elegante Vorlage präsentiert vier verschiedene Darstellungen quadratischer Funktionen mit unterschiedlichen geometrischen Eigenschaften. Meisterhaft visualisiert werden Normalparabeln, Tangenten, Achsenschnittpunkte, Symmetrieachsen und charakteristische Punkte wie Scheitelpunkt und Brennpunkt. Die Darstellungen umfassen sowohl nach oben als auch nach unten geöffnete Parabeln und zeigen die Schönheit mathematischer Symmetrie.
b) Wissenschaftliche Prinzipien
- Funktionstheorie verstehen: f(x) = ax² + bx + c mit verschiedenen, spannenden Parameterausprägungen
- Scheitelpunktform beherrschen: f(x) = a(x-h)² + k zur eleganten Identifikation von Transformationen
- Nullstellenberechnung meistern: p-q-Formel und quadratische Ergänzung sicher anwenden
- Symmetrieeigenschaften schätzen: Perfekte Achsensymmetrie bezüglich der Scheitelpunktgeraden
- Extremwertprobleme lösen: Praktische Optimierungsaufgaben mit quadratischen Funktionen
c) Schulkontext
Zielgruppe: Sekundarstufe I (Klassen 8-10) und Sekundarstufe II (Klassen 11-12)
Lehrplanbezug: Kernbestandteil aller Bundesländer im Bereich "Funktionale Zusammenhänge". Hochrelevant für das Zentralabitur in allen deutschen Bundesländern.
Fächerintegration: Mathematik, Physik (Wurfparabeln, Optik), Wirtschaft (Gewinn- und Kostenfunktionen optimieren)
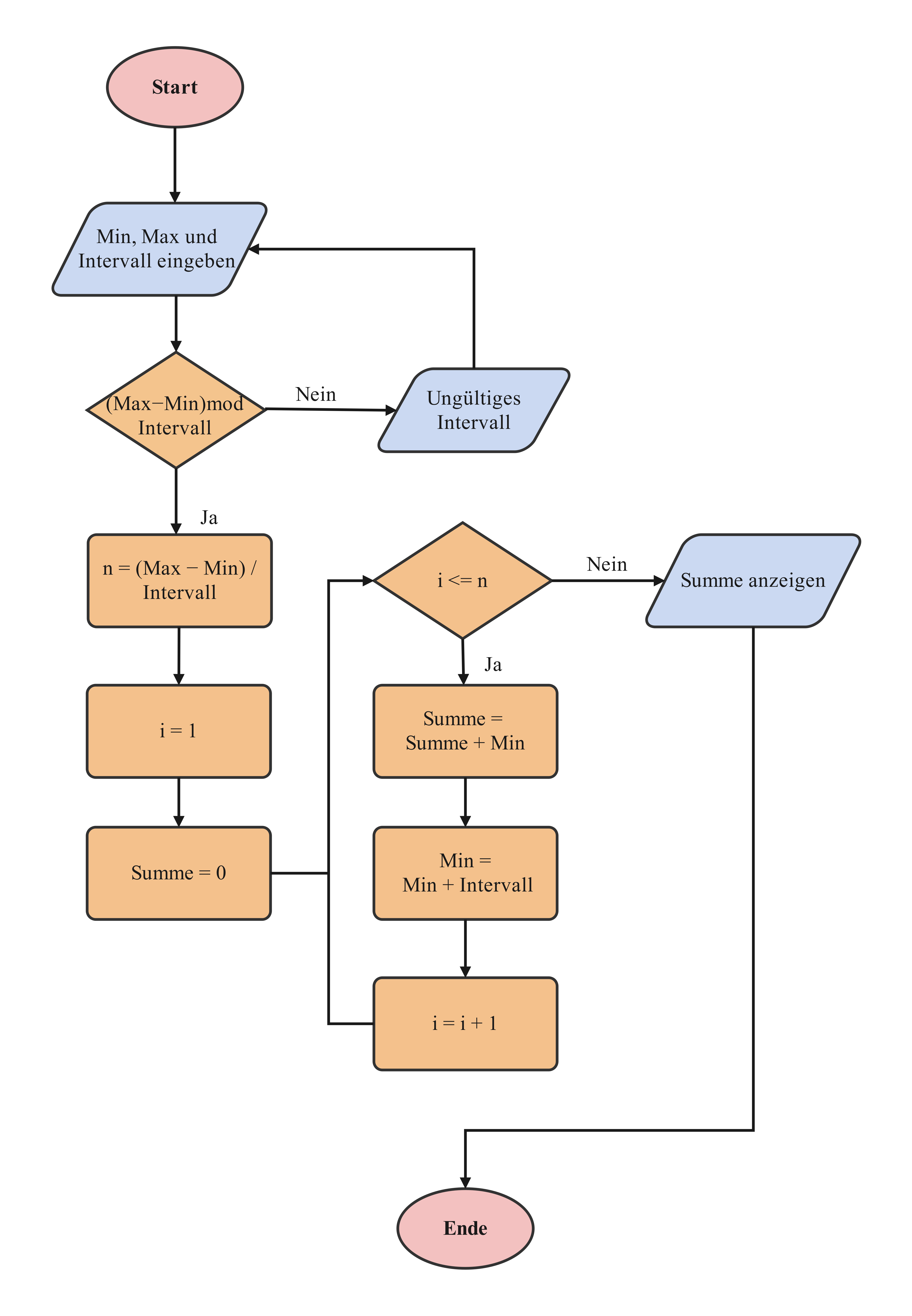
1.6 Flussdiagramm – Arithmetische Summenberechnung 🔄
a) Vorlagenbeschreibung
Dieses strukturierte Flussdiagramm veranschaulicht einen eleganten Algorithmus zur Berechnung arithmetischer Summen in einem definierten Intervall. Der Algorithmus prüft intelligent die Gültigkeit der Eingabeparameter (Min, Max, Intervall), führt dann eine effiziente iterative Summation durch und gibt das präzise Ergebnis aus. Entscheidungsknoten, Verarbeitungsschritte und Ein-/Ausgaben sind klar strukturiert und leicht verständlich dargestellt.
b) Wissenschaftliche Prinzipien
- Algorithmik beherrschen: Strukturierte Problemlösung und logische Programmlogik entwickeln
- Schleifen verstehen: Effiziente iterative Verfahren und durchdachte Laufzeitanalyse
- Arithmetische Folgen anwenden: Gaußsche Summenformel und elegante Rekursion nutzen
- Kontrollstrukturen meistern: Bedingte Anweisungen und professionelle Fehlerbehandlung
- Modularität leben: Klares Eingabe-Verarbeitung-Ausgabe-Prinzip umsetzen
c) Schulkontext
Zielgruppe: Sekundarstufe II (Klassen 10-12), Informatik-Grund- und Leistungskurse
Lehrplanbezug: Zentraler Bestandteil der Informatik-Lehrpläne aller Bundesländer im Bereich "Algorithmen und Programmierung". Hochrelevant für das anspruchsvolle Zentralabitur Informatik.
Fächerintegration: Informatik (Kernfach), Mathematik (Folgen und Reihen), Technik (intelligente Prozesssteuerung)
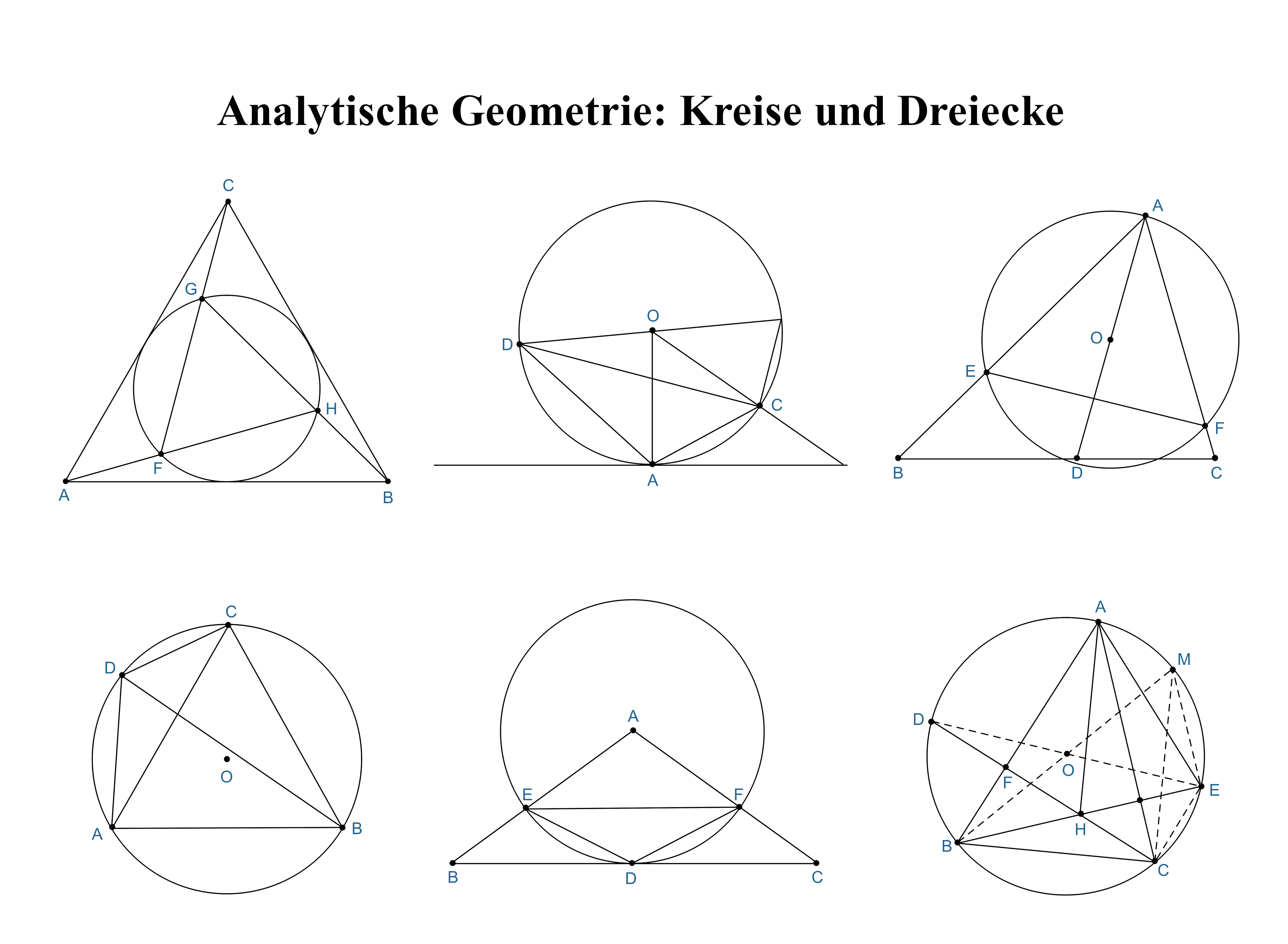
1.7 Analytische Geometrie: Kreise und Dreiecke ⭕
a) Vorlagenbeschreibung
Diese faszinierende Vorlage präsentiert sechs elegante geometrische Konstruktionen, die die fundamentalen und wunderschönen Beziehungen zwischen Dreiecken und Kreisen veranschaulichen. Meisterhaft dargestellt werden Umkreise, Inkreise, Tangenten, Winkelhalbierende und spezielle Punkte wie Umkreismittelpunkt (O) und Inkreismittelpunkt (G). Die Konstruktionen offenbaren sowohl einbeschriebene als auch umbeschriebene Kreise bei verschiedenen Dreieckstypen - ein wahres Fest der Geometrie!
b) Wissenschaftliche Prinzipien
- Umkreis-Theorie entdecken: Jedes Dreieck besitzt genau einen Umkreis - eine elegante Eigenschaft, deren Mittelpunkt am Schnittpunkt der Mittelsenkrechten liegt
- Inkreis-Eigenschaften verstehen: Der Inkreismittelpunkt liegt harmonisch im Schnittpunkt der Winkelhalbierenden
- Tangentensätze anwenden: Faszinierende Berührungseigenschaften zwischen Kreisen und Geraden
- Kongruenz- und Ähnlichkeitssätze beherrschen: Präzise geometrische Beziehungen in ebenen Figuren
- Koordinatengeometrie meistern: Moderne analytische Darstellung geometrischer Objekte
c) Schulkontext
Zielgruppe: Sekundarstufe II (Klassen 11-13), Leistungskurs Mathematik
Lehrplanbezug: Perfekt abgestimmt auf die KMK-Standards für analytische Geometrie. Besonders wertvoll für Baden-Württemberg (Bildungsplan 2016), Bayern (LehrplanPLUS), Nordrhein-Westfalen (Kernlehrplan Mathematik) und alle Bundesländer im Bereich "Geometrie und Messung".
Fächerintegration: Mathematik (Kernfach), Physik (Optik, Mechanik), Technik (professionelle CAD-Konstruktion)
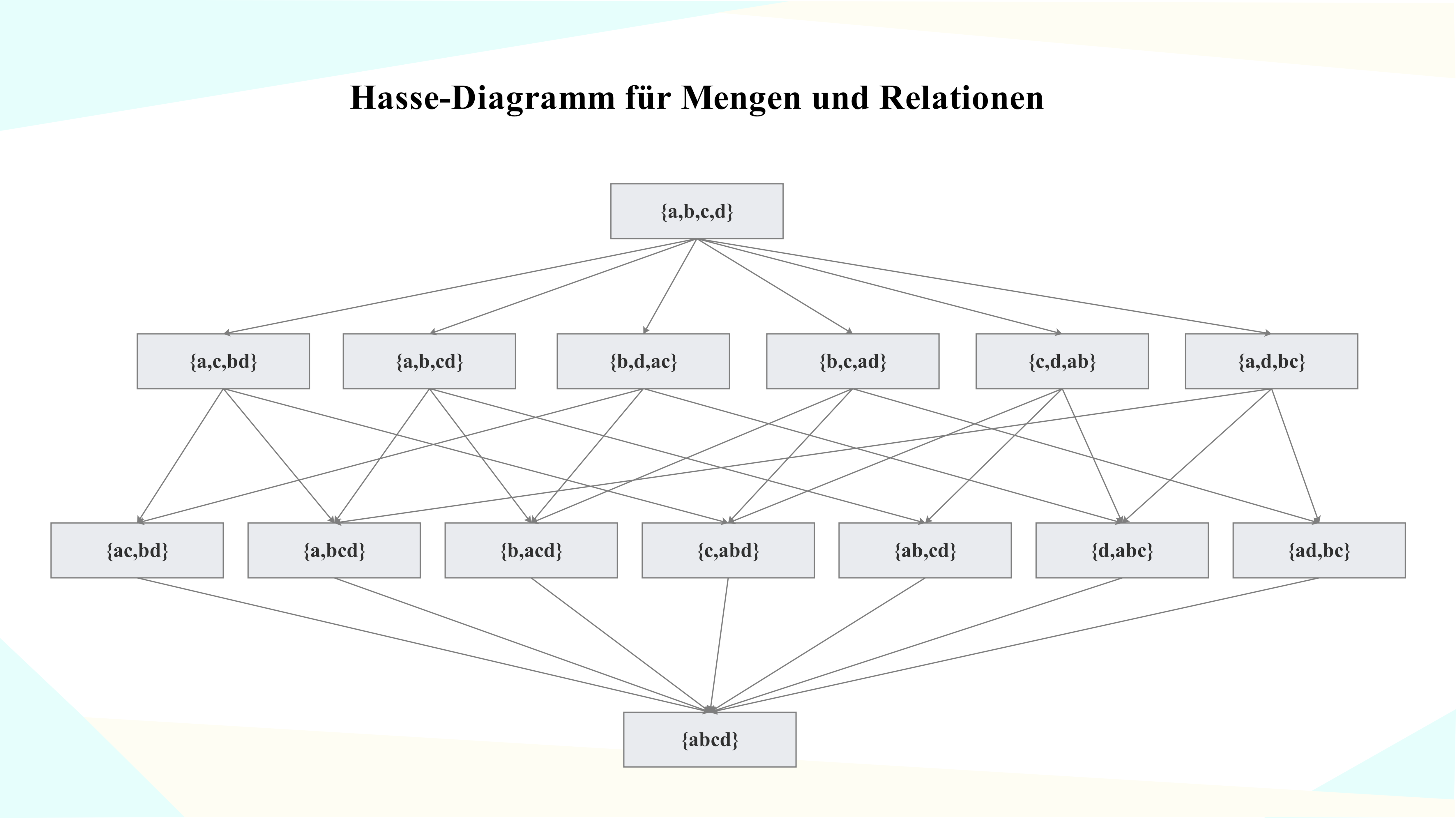
1.8 Hasse-Diagramm für Mengen und Relationen 🔗
a) Vorlagenbeschreibung
Dieses intellektuell anregende Diagramm stellt eine partielle Ordnung mittels eines elegant strukturierten Hasse-Diagramms dar und visualisiert komplexe Hierarchien sowie Inklusionsbeziehungen zwischen Mengen. Die Knoten repräsentieren Elemente einer geordneten Menge, während die durchdachten Verbindungslinien die Ordnungsrelationen ohne Transitivität darstellen - ein perfektes Werkzeug für logisches Denken!
b) Wissenschaftliche Prinzipien
- Partielle Ordnung verstehen: Reflexivität, Antisymmetrie und Transitivität systematisch erfassen
- Hasse-Diagramm-Regeln beherrschen: Minimale, übersichtliche Darstellung ohne redundante Kanten
- Supremum und Infimum entdecken: Kleinste obere und größte untere Schranken elegant bestimmen
- Verbände und Gitter erforschen: Algebraische Strukturen mit Join- und Meet-Operationen
- Topologische Sortierung anwenden: Lineare Erweiterung partieller Ordnungen meistern
c) Schulkontext
Zielgruppe: Sekundarstufe II (Klassen 12-13), Leistungskurs und Begabtenförderung
Lehrplanbezug: Bereicherung des Wahlpflichtbereichs "Diskrete Mathematik" in Bayern, Baden-Württemberg und Sachsen. Exzellente Ergänzung zu den Themen Mengenlehre und logische Strukturen.
Fächerintegration: Mathematik, Informatik (fortgeschrittene Datenstrukturen), Philosophie (formale Logik)
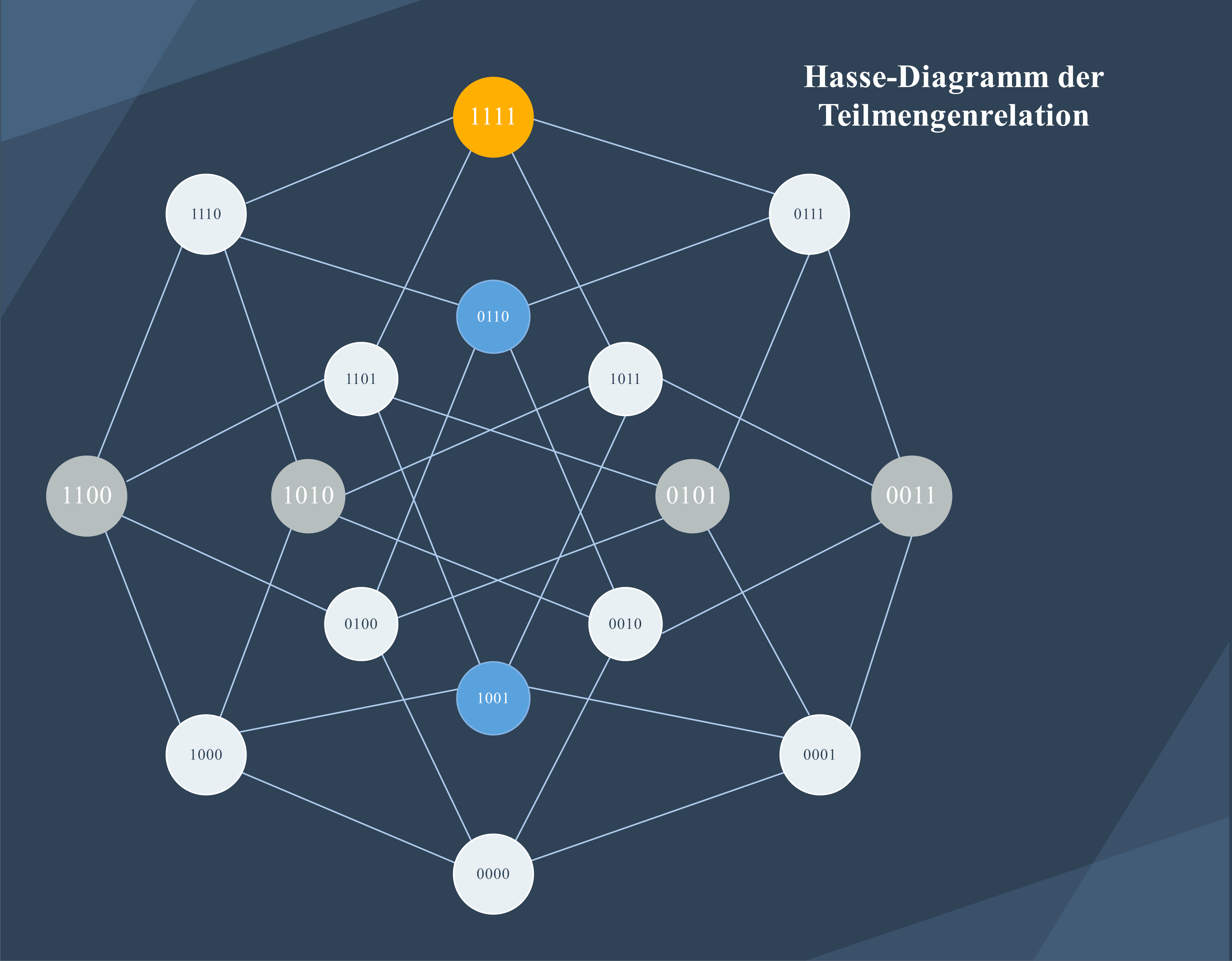
1.9 Hasse-Diagramm der Teilmengenrelation 🔢
a) Vorlagenbeschreibung
Diese hochspezialisierte und faszinierende Variante zeigt ein perfekt strukturiertes Hasse-Diagramm für ein vierstelliges Binärsystem (0000 bis 1111). Jeder Knoten repräsentiert eine Teilmenge einer vierelementigen Grundmenge, dargestellt durch elegante Binärvektoren. Die intelligenten Verbindungen illustrieren kristallklar die Inklusionsbeziehungen zwischen den Teilmengen - ein Meisterwerk der diskreten Mathematik!
b) Wissenschaftliche Prinzipien
- Binäre Codierung beherrschen: Brillante Darstellung von Teilmengen durch Charakteristikfunktionen
- Potenzmenge verstehen: Die faszinierende Menge aller Teilmengen einer gegebenen Menge
- Hamming-Distanz anwenden: Präzise Anzahl der Unterschiede zwischen Binärstrings
- Boolescher Verband erforschen: Elegante algebraische Struktur mit Komplement, Vereinigung und Durchschnitt
- Kombinatorik erleben: Spannende Binomialkoeffizienten und kreative Auswahlprobleme
c) Schulkontext
Zielgruppe: Sekundarstufe II (Klassen 12-13), anspruchsvolle Informatik-Profilkurse
Lehrplanbezug: Kernbestandteil der Informatik-Lehrpläne aller Bundesländer im Bereich "Datenrepräsentation". Hochrelevant für das anspruchsvolle Abitur Informatik in Bayern, Nordrhein-Westfalen und Baden-Württemberg.
Fächerintegration: Informatik (Kernfach), Mathematik (diskrete Strukturen), Technik (moderne Digitaltechnik)
Umfassende Vergleichstabelle
| Vorlagenname | Zielgruppe | Hauptfach | Schwierigkeitsgrad | Zeitaufwand | Bundesland-Relevanz | Zentrale Lernziele |
|---|---|---|---|---|---|---|
| 🕐 Uhrzeiten ablesen | Primarstufe (1-3) | Mathematik/Sachkunde | ⭐ Niedrig | 15-25 Min | Alle Bundesländer | Zeitverständnis entwickeln, Alltagskompetenz stärken |
| 🍕 Bruch-Darstellungen | Primarstufe (3-6) | Mathematik | ⭐⭐ Niedrig-Mittel | 20-30 Min | Alle Bundesländer | Zahlverständnis erweitern, Visualisierung fördern |
| 📐 Pythagoras-Übungen | Sek I (8-9) | Mathematik | ⭐⭐⭐ Mittel | 30-45 Min | Alle Bundesländer | Geometrisches Denken, praktische Anwendungen |
| 🗺️ Mathematik-Mindmap | Sek I/II (7-13) | Mathematik | ⭐⭐ Niedrig-Mittel | 30-60 Min | Alle Bundesländer | Systematisierung, strukturiertes Überblickswissen |
| 📈 Quadratische Funktionen | Sek I/II (8-12) | Mathematik | ⭐⭐⭐ Mittel-Hoch | 45-90 Min | Alle Bundesländer | Funktionales Denken, Extremwertprobleme meistern |
| 🔄 Algorithmus-Flussdiagramm | Sek II (10-12) | Informatik | ⭐⭐⭐ Mittel-Hoch | 45-90 Min | Alle mit Informatik-Unterricht | Algorithmisches Denken, strukturierte Problemlösung |
| ⭕ Analytische Geometrie | Sek II (11-13) | Mathematik LK | ⭐⭐⭐⭐ Hoch | 90-135 Min | Alle, bes. BY, BW, NW | Raum-Lage-Beziehungen, Koordinatengeometrie |
| 🔗 Hasse-Diagramm (Mengen) | Sek II (12-13) | Mathematik/Informatik | ⭐⭐⭐⭐ Hoch | 45-60 Min | BY, BW, SN (Wahlpflicht) | Logisches Denken, komplexes Strukturverständnis |
| 🔢 Binäres Hasse-Diagramm | Sek II (12-13) | Informatik | ⭐⭐⭐⭐ Hoch | 60-90 Min | Alle mit Informatik-Abitur | Datenrepräsentation, fortgeschrittene Algorithmik |
Empfehlungen für maximalen Lernwert
3.1 Didaktische Hinweise
Konstruktivistische Lernansätze
- Scaffolding: Systematischer Aufbau vom Konkreten zum Abstrakten
- Multiple Repräsentationen: Kombination visueller, symbolischer und verbaler Darstellungen
- Connecting Learning: Verknüpfung mit bereits erworbenen Kompetenzen
- Problembasiertes Lernen: Realitätsbezogene Anwendungssituationen
Methodische Umsetzung nach deutschen Standards
- Integration der KMK-Bildungsstandards für prozessbezogene Kompetenzen
- Berücksichtigung der Niveaukonkretisierungen (GeR-Niveau für Fremdsprachen adaptiert)
- Einbindung digitaler Medien entsprechend dem DigitalPakt Schule
- Inklusive Beschulung nach UN-Behindertenrechtskonvention
3.2 Differenzierungsmöglichkeiten
Quantitative Differenzierung
- Aufgabenumfang: Reduktion/Erweiterung der Übungsanzahl je nach Leistungsstand
- Zeitrahmen: Flexible Bearbeitungszeiten mit individuellen Zielsetzungen
- Komplexitätsstufung: Gestufte Hilfen nach dem Prinzip der minimalen Hilfe
Qualitative Differenzierung
- Lerntypen-Orientierung: Visuelle, auditive und kinästhetische Zugänge
- Sprachsensibilität: Mehrsprachige Erklärungen für DaF/DaZ-Lernende
- Begabungsförderung: Vertiefende Transferaufgaben für hochbegabte Schüler
- Inklusion: Barrierefreie Gestaltung nach WCAG 2.1-Richtlinien
3.3 Digitale Integration
Technische Umsetzung
- QR-Codes: Verknüpfung zu Online-Simulationen und interaktiven Übungen
- Augmented Reality: 3D-Visualisierungen geometrischer Körper
- Lernplattformen: Integration in Moodle, itslearning oder MS Teams
- Mobile Learning: Responsive Design für Tablet-basiertes Lernen
Kollaborative Elemente
- Peer-Review-Verfahren über digitale Lernumgebungen
- Gemeinsame Erarbeitung in virtuellen Gruppenräumen
- Dokumentation von Lernfortschritten in E-Portfolios
- Gamification durch Lernabzeichen und Fortschrittsmessung
- EdrawMax-Integration: Kollaboratives Bearbeiten von Diagrammen in Echtzeit
- Gemeinsame Vorlagenbibliotheken für Schulen und Fachschaften
3.4 Bewertungskriterien
Kompetenzorientierte Bewertung
- Prozessbewertung (40%): Lösungswege, Argumentationen, mathematische Sprache
- Ergebnisbewertung (35%): Korrektheit der mathematischen Resultate
- Anwendungsbewertung (25%): Transfer auf neue Problemstellungen
Leistungsrückmeldung nach deutschen Standards
- Transparente Bewertungsraster nach den Anforderungsbereichen I-III
- Formative Evaluation durch regelmäßige Selbsteinschätzungsbögen
- Summative Bewertung orientiert an Zentralabitur-Standards
- Individuelle Förderpläne basierend auf Kompetenzdiagnostik
Qualitätssicherung
- Peer-Review durch Fachkollegien
- Kontinuierliche Evaluation durch Schülerfeedback
- Anpassung an aktuelle Bildungsstudien (PISA, TIMSS, IQB-Bildungstrend)
- Berücksichtigung der Ergebnisse der Kultusministerkonferenz
3.5 EdrawMax im Unterrichtseinsatz
Vorteile für Lehrkräfte
- Zeitersparnis: Vorgefertigte, curriculum-konforme Vorlagen reduzieren Vorbereitungszeit erheblich
- Flexibilität: Einfache Anpassung an verschiedene Klassenstufen und Lehrplaninhalte
- Professionalität: Hochwertige, druckfertige Materialien für den sofortigen Unterrichtseinsatz
- Kollaboration: Gemeinsame Materialerstellung im Fachbereich und schulübergreifender Austausch
- Digitale Kompetenz: Moderne Unterrichtsgestaltung entsprechend dem DigitalPakt Schule
Mehrwert für Schüler
- Visualisierung: Komplexe mathematische Konzepte werden durch ansprechende Diagramme verständlicher
- Interaktivität: Eigenständige Bearbeitung und Anpassung von Vorlagen fördert aktives Lernen
- Kreativität: Entwicklung eigener mathematischer Darstellungen und Präsentationen
- Medienkompetenz: Erwerb digitaler Fähigkeiten für Studium und Beruf
- Differenzierung: Individuelle Lerngeschwindigkeit durch selbstgesteuerte Bearbeitung
Integration in den deutschen Bildungskontext
- Unterstützung der KMK-Strategie "Bildung in der digitalen Welt"
- Förderung der 21st Century Skills: Kreativität, Kollaboration, Kommunikation
- Vorbereitung auf digitale Abiturprüfungen und E-Assessments
- Beitrag zur MINT-Förderung und Studienorientierung
- Barrierefreie Gestaltung für inklusive Beschulung
3.6 Praxisempfehlungen für den Einsatz
Unterrichtsszenarien
- Einführungsstunden: Verwendung vorgefertigter Vorlagen zur Konzepteinführung
- Übungsphasen: Schülerindividuelle Anpassung und Erweiterung bestehender Diagramme
- Projektarbeit: Kollaborative Erstellung komplexer mathematischer Visualisierungen
- Prüfungsvorbereitung: Systematische Wiederholung durch strukturierte Mindmaps
- Präsentationen: Schülervorträge mit selbst erstellten EdrawMax-Diagrammen
Technische Integration
- Einbindung in bestehende Lernmanagementsysteme (Moodle, itslearning)
- Export in verschiedene Formate für Print- und Digitalmedien
- Cloud-basierte Speicherung für geräteunabhängigen Zugriff
- Kompatibilität mit interaktiven Whiteboards und Tablet-Klassen
- Offline-Funktionalität für den Einsatz ohne Internetverbindung
Fortbildungsempfehlungen
- Schulinterne Lehrerfortbildungen zur EdrawMax-Nutzung
- Fachschaftsübergreifende Workshops für MINT-Fächer
- Peer-Learning zwischen technikaffinen und weniger erfahrenen Kollegen
- Integration in die Lehrerausbildung an Universitäten und Seminaren
- Kontinuierliche Weiterbildung entsprechend Software-Updates
Fazit und Ausblick
Die vorgestellten neun mathematischen Lernvorlagen, erstellt mit EdrawMax, decken das gesamte Spektrum vom Primarbereich bis zur Sekundarstufe II ab und entsprechen den aktuellen Bildungsstandards aller deutschen Bundesländer. Durch die systematische Integration digitaler Medien, differenzierte Lernzugänge und kompetenzorientierte Bewertungsverfahren werden optimale Lernbedingungen für heterogene Schülergruppen geschaffen.